After using some neural networks to analyse a small set of data for a friends pet project, I will focus on my own data.
I have a web scraper, StockReader, that collects some information about public stocks that are listed in Sweden. That has been in use for eight years and I have more than 1500 snapshots of a couple of hundreds of stocks.
It was originally written in C++ (the code was terrible, but it was essential for me to learn to build a more complex program) and I later ported that to a twenty-four line python script that is scheduled to run three times a week.
Now, I want to use the data to learn more about machine learning and analysis of time series. I also want to get experience from C#/Visual Studio and Angular JS.
I don't expect to find a magic algorithm that helps me in stock-picking. The purpose of this project is to learn coding, machine learning, C#, Visual Studio and Angular JS.
The Different Technology Areas for the Project
The data is saved in csv files (comma separated values). The data includes stock price, earnings per share, dividends, profit margin, RSI and date for the quarterly reports.
I will create a Windows program based on C# in Visual Studio to populate a mySQL database with the stock data. It would probably be easier using Python but I want to explore new tools and programming languages.
After the data is in the database, I will build a web app using Angular JS, That program will check the data and search for possible stock splits and inconsistent data.
Once the data is corrected, I will analyse it. Since Python has very powerful AI packages, I will use Python to extend the web app above.
I will start by describing the data and some relevant topics for stock markets.
Saturday, 27 April 2019
Saturday, 20 April 2019
Machine Learning: Using a Neural Network for Value Prediction
Until now, I've been using a Neural Network for a binary classification. Predicting a continuous value would be more relevant for my case.
I found an example that is using the sckit-learn package.
The Peer Project
This time, I've made some changes to the input data:
The error messages are reoccurring and indicates that the convergence is too weak. It seems not to be any easy-detectable link between inputs and the magnitude of the output.
I tested with a test size of 0.2 (6 or 7 samples in training set and 1 or 2 samples in test set):
One iteration:
I found an example that is using the sckit-learn package.
The Peer Project
This time, I've made some changes to the input data:
- I will make the neural network train for the actual training output data instead of a binary representation of that data.
- I will sort the training input data in three groups of thirteen values:
 |
| The values are initially arranged in triplets (likelihoods for events 1, X and 2) for thirteen samples. |
I sorted the array by descending values with a simple modification of the numpy sort command:
I use the MLPRegressor with some different random seeds and 10000 iterations.
The results are a bit disappointing. For some random seeds (and different sets of training/test data), the errors are smaller after 10000 iterations, compared to after one iteration.
 |
| Seed 300, 10000 iterations. |
 |
| Seed 400, 1 iteration |
 |
| Seed 400, 10000 iterations |
 |
| Seed 400, 1 iteration |
The error messages are reoccurring and indicates that the convergence is too weak. It seems not to be any easy-detectable link between inputs and the magnitude of the output.
Adding more iterations seems not to be the magical solution either.
 |
| For 20 000 iterations, the error is smaller than for 10 000 iterations. But for 40 000 iterations, the error is increasing. |
It seems that it is very important to be able to interpret the neural networks!
Checking a Known Data Set
As a sanity check, I've been training the MLPRegressor on a small training set:
 |
| This sample should be quite easy for an neural network to train. |
One iteration:
 |
| The MLPRegressor wasn't able to converge after one sample. This makes sense, since it takes quite a number of iterations to converge. |
Ten iterations:
 |
| I still see the warning about convergence, but the errors are smaller. This means that the algorithm is converging after all |
A Thousand Iterations:
| The error isn't shown anymore, and the errors are smaller now. |
A Million Iterations:
 |
| Here, I'm running twice on the same setup. The first optimization converged much more poorly than the second one. The reason for this is probably an unfortunate selection of training data. |
The example above illustrates how important it is to have a big set of data to test and train on.
I'll finish this part of my Neural Network project for now. The next project will start in the next blog post and cover much more training data.
Saturday, 13 April 2019
Machine Learning: Tweaking the Hidden Layer
In the last blog post, I used a neural network with a hidden layer to try to predict a binary outcome based ion some input data. Now, I'll investigate how different sizes of the hidden layer will affect the output of the network.
Keep in mind that:
- I'm learning about neural networks - this blog describes my learning curve and not recommended ways of handling neural networks.
- Different shapes and depths of neural networks work for different problems, there is no "Golden" neural network.
- The data I'm using for this example is probably random in the sense that there is likely no obvious connection between input and output.
10 Neurons in Hidden Layer:
(the setting from the last blog post): The neural network was well fitted for the training set, but worse than guessing for the test set.
1 Neuron in Hidden layer:
This is practically a single-layer neural network. For the training set, the predictions are accurate for the "ones", but the predictions are 0.5 for the other values. This means that the neural network fails to predict "zero" at all. The prediction "0.5" can be seen as an attempt by the neural network to predict zero.
2 Neurons in Hidden Layer:
The predictions on the training set is better, but two predictions are still at 0.5 (samples 9 and 23). For the test set, the network is confident but wrong in six cases out of eight.
4 Neurons in Hidden Layer:
Now, the neural network fits to the training set (no errors). This has a similar confusion matrix as the neural network above, with 2 neurons in the hidden layer.
8+ Neurons in Hidden Layer:
The network is very confident all the times, but the test predictions are bad. This indicates that the neural network is well fitted to the training data (and that the sigmoid function is narrow enough to make the estimates ones or zeros). Adding more nodes makes the estimates more confident, but not more correct.
Matrix Calculations:
I've made a summary of the matrix calculations below:
Some Findings:
A neural network should have a general understanding of the input, and it should ideally be less confident.
This exercise illustrates one of the dangers with neural networks: it can generate very nice predictions that have low uncertainties, but fail to predict new data. It can give us an illusion of seeing patterns that doesn't exist.
There is a risk that a sum-optimal neural network will tell us what we want to hear. This makes it very important to look at the results with an open and still critical mind set.
Saturday, 6 April 2019
Machine Learning: Adding a Layer to a Neural Network
After creating an extremely simple neural network from an example, I've spent some time learning more about neural networks.
For the second project, I have 26 (or possibly 39) input data points per sample. Those inputs values shall map to one output value. I want to investigate whether it is possible to predict the order of magnitude of that output value.
I'll use the python code from Milo Spencer-Harber and his article.
I have no clue how (or if at all) the input is related to the output. It is very likely a stochastic process, but I want to see if a neural network can find any connection or predictability between input and output. For this example, I need something more advanced than a single-layer neural network.
A single-layer neural network has some built-in flaws. For example, it can not model a XOR gate. A XOR gate is an exclusive or.
I'll use a two-layer neural network with 26 (or 39) input nodes, a hidden layer with 10-ish nodes and one output node.
A simpler image will illustrate the connections
The hidden layer is connected to the input nodes with 26*10=260 connections. The output is connected to the hidden layer with ten nodes. This makes 270 connections that shall be updated for each iteration.
The First Sessions Using the Neural Network
I arranged the input data in the form of a matrix (a numpy array of arrays) where each row contains one set of input data. Since the script that I used could handle matrixes, the calculations were done very quickly - all sets of input data were calculated simultaneously.
It took the algorithm 1.7 seconds to perform 60 000 iterations of 30 sets of input data, each containing 26 floats. The machine that I use has a i5-8250U/1.6GHz CPU with 8 GB RAM - a low-end laptop.
The confusion matrix indicates that I'd be better off guessing. Since I know that chance is a very big part of the results, I'm not surprised. The algorithm has told me that the output is likely not predictable.
When increasing the hidden layer from 10 to 20 neurons (two times more complex), the algoritm needed 2.2 seconds to complete. So it is clear that well-crafted algorithms (like the one created by Milo) are essential.
From the results, it initially seems that the neural network fitted successfully to the training set (row 1-30). When predicting the test set, the network performed poorly. This looks like an overfitted neural network. I start to doubt whether it is possible to predict the outcome using the input data, but I will do some more attempts.
Lessons learned:
Next steps:
For the second project, I have 26 (or possibly 39) input data points per sample. Those inputs values shall map to one output value. I want to investigate whether it is possible to predict the order of magnitude of that output value.
I'll use the python code from Milo Spencer-Harber and his article.
I have no clue how (or if at all) the input is related to the output. It is very likely a stochastic process, but I want to see if a neural network can find any connection or predictability between input and output. For this example, I need something more advanced than a single-layer neural network.
A single-layer neural network has some built-in flaws. For example, it can not model a XOR gate. A XOR gate is an exclusive or.
I'll use a two-layer neural network with 26 (or 39) input nodes, a hidden layer with 10-ish nodes and one output node.
 |
| 26-10-1 layers. The input nodes (input data) are on the lower part of the graph, the hidden layer in the middle and the output on the top. |
 |
| Each input is connected to each node on the hidden layer. |
The First Sessions Using the Neural Network
I arranged the input data in the form of a matrix (a numpy array of arrays) where each row contains one set of input data. Since the script that I used could handle matrixes, the calculations were done very quickly - all sets of input data were calculated simultaneously.
It took the algorithm 1.7 seconds to perform 60 000 iterations of 30 sets of input data, each containing 26 floats. The machine that I use has a i5-8250U/1.6GHz CPU with 8 GB RAM - a low-end laptop.
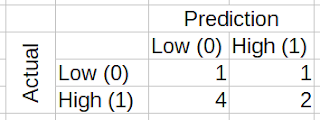
 |
| Samples 1-30 are the training set. The last eight samples are the test set. I missed five out of six "High" values, and I missed one of two "Low" values. |
When increasing the hidden layer from 10 to 20 neurons (two times more complex), the algoritm needed 2.2 seconds to complete. So it is clear that well-crafted algorithms (like the one created by Milo) are essential.
 |
| This time, I missed four of six "High" values in and one of two "Low" values in the test set. |
Lessons learned:
- Execution speed depends a lot on the implementation. Arranging input data into matrices and clever use of built in functions will be crucial for this project - master your Python-Fu!
- Neural Networks are tools that can try to adopt a couple of matrices to a set of learning data. If the data is flawed (too little data, biased data or random data), the outcome won't be better than the input data.
Next steps:
- I need to get a better understanding on how the size of the hidden layer will affect the output - what happens with a very small hidden layer (approaching a single-layer neural network)? And what happens when I add many nodes in the hidden layer?
- I will also rearrange the input data to see if the neural network will be more successful analyzing decreasing series of likelihoods.
- So far, I have a threshold to distinguish "low" outputs from "high" output values. I need to learn how to make a neural network predict a value on a continuous scale instead.
Subscribe to:
Comments (Atom)