Machine Learning: Adding a Layer to a Neural Network

After creating an extremely simple neural network from an example, I've spent some time learning more about neural networks.

For the second project, I have 26 (or possibly 39) input data points per sample. Those inputs values shall map to one output value. I want to investigate whether it is possible to predict the order of magnitude of that output value.

I'll use the python code from Milo Spencer-Harber and his article.

I have no clue how (or if at all) the input is related to the output. It is very likely a stochastic process, but I want to see if a neural network can find any connection or predictability between input and output. For this example, I need something more advanced than a single-layer neural network.

A single-layer neural network has some built-in flaws. For example, it can not model a XOR gate. A XOR gate is an exclusive or.

I'll use a two-layer neural network with 26 (or 39) input nodes, a hidden layer with 10-ish nodes and one output node.

26-10-1 layers.
The input nodes (input data) are on the lower part of the graph,
the hidden layer in the middle and the output on the top.

A simpler image will illustrate the connections

Each input is connected to each node on the hidden layer.

The hidden layer is connected to the input nodes with 26*10=260 connections. The output is connected to the hidden layer with ten nodes. This makes 270 connections that shall be updated for each iteration.

The First Sessions Using the Neural Network 
I arranged the input data in the form of a matrix (a numpy array of arrays) where each row contains one set of input data. Since the script that I used could handle matrixes, the calculations were done very quickly - all sets of input data were calculated simultaneously.

It took the algorithm 1.7 seconds to perform 60 000 iterations of 30 sets of input data, each containing 26 floats. The machine that I use has a i5-8250U/1.6GHz CPU with 8 GB RAM - a low-end laptop.

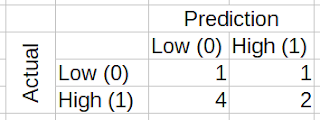
Samples 1-30 are the training set. The last eight samples are the test set.
I missed five out of six "High" values, and I missed one of two "Low" values.

The confusion matrix indicates that I'd be better off guessing. Since I know that chance is a very big part of the results, I'm not surprised. The algorithm has told me that the output is likely not predictable.

When increasing the hidden layer from 10 to 20 neurons (two times more complex), the algoritm needed 2.2 seconds to complete. So it is clear that well-crafted algorithms (like the one created by Milo) are essential.

This time, I missed four of six "High" values in and one of two "Low" values in the test set. 

From the results, it initially seems that the neural network fitted successfully to the training set (row 1-30). When predicting the test set, the network performed poorly. This looks like an overfitted neural network. I start to doubt whether it is possible to predict the outcome using the input data, but I will do some more attempts.

Lessons learned:

• Execution speed depends a lot on the implementation. Arranging input data into matrices and clever use of built in functions will be crucial for this project - master your Python-Fu!
• Neural Networks are tools that can try to adopt a couple of matrices to a set of learning data. If the data is flawed (too little data, biased data or random data), the outcome won't be better than the input data. 

Next steps:

• I need to get a better understanding on how the size of the hidden layer will affect the output - what happens with a very small hidden layer (approaching a single-layer neural network)? And what happens when I add many nodes in the hidden layer?
• I will also rearrange the input data to see if the neural network will be more successful analyzing decreasing series of likelihoods.
• So far, I have a threshold to distinguish "low" outputs from "high" output values. I need to learn how to make a neural network predict a value on a continuous scale instead.