Classification
Many machine learning problems are concerning Classification. That may be "dirty/clean", malignant/benign tumor, spam/no spam email etc.
In this case, the training output y will be either zero (negative class) or one (positive class) for the two class case.
Logistic Regression / Hypothesis Representation
Logistic regression model is improved with a sigmoid function:
The sigmoid function offers a smooth transition from 0 (z << 0) to 1 (z >> 0).
hθ(x) is the probability for a positive result, given the input x.
Decision Boundary
A decision boundary is the limit between the set of x that results in hθ(x)>0.5 and the set of hθ(x)<0.5
Cost Function
Simplified Cost Function and Gradient Descent
For the two binary cases for the cost function (y=0 and y=1), the cost function can be written as:
This function be derived using maximum likelihood estimation.
The optimization problem is now to minimize J with respect to the parameters and the observations.
The gradient descent method will update the parameters with the error multiplied by the observations:
Advanced Optimization
Another optimization algorithms are
- Gradient Descent
- Conjugate Gradient
- BFGS
- L-BFGS
Regularization
Too many features in the hypothesis may cause overfitting. That means that the model fits the training set perfectly but misses out in new cases. There are two ways to handle overfitting:
- Reducing number of features (manually or using a selection algorithm)
- Regularization (keep all features but reduce magnitude of theta)
Regularization will add the sizes of some hypothesis parameters to the cost function. The first theta parameter will not be optimized by convention.
The vector form will be:

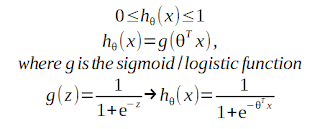






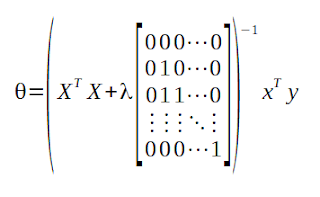
No comments:
Post a Comment